O crescimento de uma população está sujeito às várias limitações impostas pelo meio, tais como: competição, predatismo, parasitismo, espaço, alimentos, etc. O estudo de crescimento populacional proposto por Verhulst leva em consideração algumas destas variáveis, ao contrário do modelo malthusiano, que leva em consideração apenas a capacidade de reprodução da espécie estudada. Quando comparadas, as curvas de crescimento de cada um dos modelos mencionados são completamente distintas. A curva obtida no modelo de Verhulst se parece com um S (curva S ou curva de crescimento real) enquanto aquela obtida com o modelo de Malthus se assemelha a um J (curva J ou curva de potencial biótico). Para saber mais sobre estes dois modelos de crescimento populacional veja o tópico "Dinâmica populacional".
A curva J, como já dissemos anteriormente, despreza qualquer resistência ao crescimento da população, enquanto a curva S considera algumas variáveis inibidoras deste crescimento. Quando comparamos as duas curvas temos condições de observar os efeitos causados no crescimento populacional quando consideramos alguns inibidores. A Figura 1 nos mostra as duas curvas e destaca uma região delimitada pelas curvas J e S e ainda dentro dos limites da capacidade de limite (suporte) do meio. A área desta região é que chamamos de resistência do ambiente ou resistência do meio, Figura 1.
A curva J, como já dissemos anteriormente, despreza qualquer resistência ao crescimento da população, enquanto a curva S considera algumas variáveis inibidoras deste crescimento. Quando comparamos as duas curvas temos condições de observar os efeitos causados no crescimento populacional quando consideramos alguns inibidores. A Figura 1 nos mostra as duas curvas e destaca uma região delimitada pelas curvas J e S e ainda dentro dos limites da capacidade de limite (suporte) do meio. A área desta região é que chamamos de resistência do ambiente ou resistência do meio, Figura 1.
Figura 1
A resistência oferecida pelo meio é portanto a área da região limitada pela capacidade de suporte do meio, pela curva de potencial biótico e pela curva de crescimento real. As curvas do modelo de Verhulst e do modelo de Malthus são obtidas, respectivamente, por meio das seguintes funções:
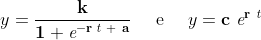onde k é uma constante positiva que representa a capacidade de suporte do meio, r é a taxa intrínseca de crescimento, a uma constante de ajuste à espécie em questão e 
é a população inicial.
Com auxílio do applet abaixo tente compreender a relação entre a curva de potencial biótico, a curva de crescimento real e a resistência do ambiente. Anote todas as suas conclusões! Biologicamente, as conclusões fazem sentido?
Com auxílio do applet abaixo tente compreender a relação entre a curva de potencial biótico, a curva de crescimento real e a resistência do ambiente. Anote todas as suas conclusões! Biologicamente, as conclusões fazem sentido?
Para obter numericamente a resistência do ambiente é necessário encontrar a área de uma região que não se parece com nenhuma das figuras elementares da geometria plana (triângulo, retângulo, trapézio, etc). Como poderíamos então encontrar este valor? Para isso deverímos ser capazes de calcular a área de uma região delimitada por curvas. Supondo que isso seja possível poderíamos tentar obter a área desejada, Área 3 da Figura 2, subtraindo a Área 2 da Área 1, Figura 2.
Figura 2
Mas isso ainda não resolve o nosso problema, pois não sabemos como calcular as áreas 1 e 2. Vamos então calcular a Área 2 tentando aproxima-la a alguma figura geométrica conhecida, retângulos, por exemplo, Veja na Figura 3 - (A) uma aproximação da Área 2 por 5 retângulos. Desta forma podemos observar que a soma da área de cada um dos 5 retângulos nos fornece uma aproximação para a Área 2. Na segunda imagem, Figura 3 - (B), também foi realizada uma aproximação por retângulos, mas desta vez foram utilizados 10 retângulos em vez de 5. Note que a soma das áreas dos retângulos da segunda imagem está mais próximo da área desejada do que a soma das áreas dos retângulos da primeira imagem. Se em vez de 10 utilizássemos 50 retângulos, Figura 3 - (C), o que aconteceria com soma da área desses retângulos se comparada com a área procurada? E se em vez de 50 utilizássemos 100 ou até mesmo 1 000 retângulos?
Figura 3
É evidente que aumentando a quantidade de retângulos a soma de suas áreas também aumentará e se aproximará cada vez mais da área da região grifada. De modo geral, se n é o número de retângulos utilizados para aproximar a Área 2 então podemos dizer que a soma das áreas dos n retângulos tende a se aproximar do valor procurado na medida que n aumenta (simbolicamente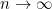 
). Mais precisamente, se denotarmos a área do primeiro retângulo por A1, do segundo por A2, do terceiro por A3, ... e a área do n-ésimo retângulo por An, então a Área 2 será aproximadamente a soma
A1 + A2 + A3 + ... + An .
Fica claro que esta soma tende ao valor da Área 2 quando n se torna cada vez maior (
Note que o somatório da última igualdade foi construído a partir da curva S em um intervalo bem determinado do eixo x, o intervalo que limita a área desejada. No caso em estudo o intervalo tem início em 0 e se estende até aproximadamente 4.35, Figura 4. Isto é, se y = f(t) é a função cujo gráfico é a curva S então a Área 2, ou o somatório que a define, depende de y = f(t) e do intervalo [0, 4.35]. Nos casos em que o gráfico da função se encontra acima do eixo x no intervalo de interesse (função positiva no intervalo), como é o caso da região de interesse, denotamos a Área 2 da seguinte maneira
Na notação utilizada, o símbolo ∫ nos remete a uma soma enquanto os outros elementos explicitam que o somatório depende do intervalo [0, 4.35] e da função y = f(t). Alterando a função e o intervalo o resultado do somatório será outro. É claro, pois a área também será outra! A última igualdade define o que chamamos integral de 0 até 4.35 de f ( simbolicamente: %5C&space;dt "\int_{0}^{4.35}f(t)\ dt")
). Resumindo, a integral de 0 até 4.35 de f é definida como sendo o valor da Área 2.
Figura 4
De modo geral, para uma função y = f(x) positiva no intervalo [a,b] definimos a integral de a até b de f como sendo a área da região limitada pelo gráfico de f e dentro dos limites do intervalo [a,b], Figura 5. Simbolicamente, escrevemos
Figura 5
Finalmente, conhecendo esta nova ferramenta matemática chamada de integral definida podemos realizar o cálculo de área de regiões limitadas por curvas (gráficos de funções). Por exemplo, a Área 2, citada anteriormente, é limitada pela função =\frac{2}&space;{1+e^{3-2t}} "f(t)=\frac{2} {1+e^{3-2t}}")
. Logo, ela corresponde a integral 
. Utilize a calculadora abaixo e encontre seu valor.
No caso da Área 1 a curva que limita a região, Figura 6 - (A), coincide com a curva de potencial biótico até um certo ponto. Em seguida, a reta que representa o suporte do meio passa a limitar a região. Sendo assim, vamos encontrar a Área 1 dividindo a região em duas áreas menores, Figura 6 - (B). A função que determina a curva de potencial biótico é dada por&space;=&space;0.09&space;e^{2&space;t} "g(t) = 0.09 e^{2 t}")
. Sabendo disso, nos resta descobrir o ponto que divide a Área 1 em duas sub regiões. Isto pode ser feito descobrindo o valor de t que satisfaz a equação 
. Justifique esta afirmação! Uma vez entendido que a solução da equação acima é o que procuramos, podemos facilmente resolvê-la com o auxílio do WolframaAlpha, basta digitar a equação e teclar "Enter", obtendo a resposta t = 1.55. Sendo assim a primeira sub área pode ser calculada por meio da integral 
. E a outra sub área é o retângulo. Fazendo as contas, qual o valor encontrado para a resistência do meio neste caso? Anote suas dúvidas e conclusões.
No caso da Área 1 a curva que limita a região, Figura 6 - (A), coincide com a curva de potencial biótico até um certo ponto. Em seguida, a reta que representa o suporte do meio passa a limitar a região. Sendo assim, vamos encontrar a Área 1 dividindo a região em duas áreas menores, Figura 6 - (B). A função que determina a curva de potencial biótico é dada por
Figura 6
O gráfico abaixo, Figura 7, nos mostra a curva de potencial biótico e a curva S de crescimento da população de leões marinhos na costa do pacífico dos Estados Unidos. Use a calculadora de integral para determinar a resistência do meio neste caso.
Pra finalizar, será que a integral definida sempre representa a área de alguma região? Faça alguns testes... Por exemplo, com a função f (x) = - X2. Anote suas dúvidas e conclusões!
Comente com o Facebook: