Segundo Odum e Barret no livro Fundamentos de Ecologia: "A população é
uma entidade em mudança. Mesmo quando a comunidade e o ecossistema parecem não
estar mudando, densidade, natalidade, sobrevivência, estrutura etária, taxa de crescimento e outros atributos das populações componentes estão em fluxo, pois as espécies se ajustam constantemente às estações, às forças físicas e umas às outras. O estudo das mudanças no número relativo de organismos em populações e dos fatores que explicam essas mudanças é chamado de dinâmica de populações". Segundo estes mesmos autores "os ecólogos estão mais interessados em como e a que taxa a população está mudando do que em seu tamanho absoluto e composição a qualquer tempo". Como o estudo de taxa de mudança (variação) é o principal interesse deste curso veremos como este conceito nos ajuda a compreender a dinâmica das populações.
Iniciemos então com o estudo das curvas de crescimento populacional.
As populações possuem diversas características próprias, mensuráveis. Cada membro de uma população pode nascer, crescer e morrer, mas somente uma população como um todo possui taxas de natalidade e de crescimento específicas, além de possuir um padrão de dispersão no tempo e no espaço.
O tamanho de uma população pode ser avaliada pela sua densidade
A densidade populacional pode sofrer alterações. Mantendo-se fixa a área de distribuição, a população pode aumentar devido a nascimentos e imigrações. A diminuição da densidade pode ocorrer como consequência de mortes ou de emigrações.
Curvas de crescimento
A curva S é a de crescimento populacional padrão, a esperada para a maioria das populações existentes na natureza. Ela é caracterizada por uma fase inicial de crescimento lento, em que ocorre o ajuste dos organismos ao meio de vida. A seguir, ocorre um rápido crescimento, do tipo exponencial, que culmina com uma fase de estabilização, na qual a população não mais apresenta crescimento. Pequenas oscilações em torno de um valor numérico máximo acontecem, e a população, então permanece em estado de equilíbrio.
Observe o gráfico abaixo para ententer melhor:
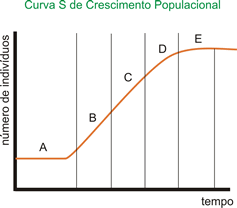
Fase A: crescimento lento, fase de adaptação da população ao ambiente, também chamada de fase lag.
Fase B: crescimento acelerado ou exponencial, também chamada de fase log. Fase C: a população está sujeita aos limites impostos pelo ambiente, a resistência ambiental é maior sobre a população. Fase D: estabilização do tamanho populacional, onde ocorre oscilações do tamanho populacional em torno de uma média. Fase E: é a curva teórica de crescimento populacional sem a interferência dos fatores de resistência ambiental. A curva J é típica de populações de algas, por exemplo, na qual há um crescimento explosivo, geométrico, em função do aumento das disponibilidades de nutrientes do meio. Esse crescimento explosivo é seguido de queda brusca do número de indivíduos, pois, em decorrência do esgotamento dos recursos do meio, a taxa de mortalidade é alta, podendo, inclusive, acarretar a extinção da população do local.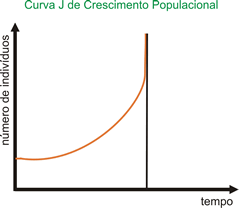 
Fatores que regulam o crescimento populacional
A fase geométrica do crescimento tende a ser ilimitada em função do potencial biótico da espécie, ou seja, da capacidade que possuem os indivíduos de se reproduzir e gerar descendentes em quantidade ilimitada. Há porém, barreiras naturais a esse crescimento sem fim. A disponibilidade de espaço e alimentos, o clima e a existência de predatismo e parasitismo e competição são fatores de resistência ambiental (ou, do meio que regulam o crescimento populacional. O tamanho populacional acaba atingindo um valor numérico máximo permitido pelo ambiente, a chamadacapacidade limite, também denominada capacidade de carga.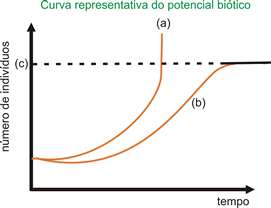 
A curva (a) representa o potencial biótico da espécie; a curva (b) representa o crescimento populacional padrão; (c) é a capacidade limite do meio. A área entre (a) e (b) representa a resistência ambiental.
|
Como vimos anteriormente o crescimento descrito pela curva J, curva de potencial biótico, é aquela que leva em consideração apenas a capacidade de reprodução dos indivíduos. Sendo assim é de se esperar que quanto maior a população, maior também será a taxa de crescimento populacional. Isto é, a taxa de crescimento (velocidade de crescimento) de uma determinada população é proporcional ao tamanho da população, já que estão sendo desprezadas as barreiras que impedem o crescimento. É claro que esta curva não será a mesma para todos os tipos de seres vivos, por exemplo, o potencial reprodutivo humano difere do potencial reprodutivo das bactérias. No entanto, em ambos os casos as taxas de crescimento serão proporcionais ao tamanho da população, quanto mais seres humanos em idade fértil, maior será o índice de reprodução. Nestas condições, o tamanho da população depende quase que exclusivamente do tempo necessário para reprodução. Digamos, por exemplo, que y = y(t) seja a quantidade de indivíduos de uma população em um determinado momento t (tempo). A taxa de variação (crescimento) de y em relação ao tempo t é o que chamamos de derivada da função y no instante t e denotamos por y' = y'(t) ou ainda 
. Sendo assim, podemos escrever
sendo r uma constante positiva que representa a capacidade de reprodução e sobrevivência e é chamada de taxa intrínseca de crescimento. Por exemplo, r = 1 significa que a taxa de crescimento é igual ao crescimento da população. Se r = 2 então a taxa de crescimento é o dobro do crescimento populacional.
A equação (I) é chamada de Equação Diferencial Ordinária (EDO) e foi proposta por Thomas Malthus, por esta razão é conhecido por modelo de Malthus. Uma solução para este modelo é uma função y = y(t) cuja derivada é igual a r vezes ela mesma, y' = r y.
Para encontrar uma função com a característica desejada, isto é, que satisfaça a equação (I), vamos recorrer ao WolframaAlpha. Abra o link anterior e digite a equação y'(t) = r y(t). Em seguida tecle "Enter", fazendo isso será exibida a função &space;=&space;c_1&space;\;&space;\textit{e}^{r&space;\;&space;t}} "\mathbf{y(t) = c_1 \; \textit{e}^{r \; t}}")
, sendo c1 um número real e e o número irracional (aproximadamente 2.72) conhecido como número de Euler (homenagem ao matemático Leonhard Euler). Use a calculadora de derivadas para derivar a função encontrada acima e verifique que ela realmente é uma solução para a equação (I).
No applet abaixo podemos ver que o gráfico da função y = c e kt nos fornece a curva J. Faça variar os valores das constantes constantes c e k e veja como se comportam os gráficos da função e de sua derivada. Anote suas conclusões! Você saberia dar uma explicação para o fato de o número de Euler ser tão especial ao ponto de ser denotado por uma letra e receber o nome de um grande matemático.
Veja na Figura 1 alguns casos de crescimento exponencial, curva J.
Figura 1
Enquanto a curva J pressupõe condições ideais, a curva S representa o crescimento da maioria das populações da natureza, por esta razão ela é também chamada de curva de crescimento real. A função que fornece a curva S é chamada de função logística e advém do modelo proposto por Verhulst. Podemos pensar este modelo a partir do modelo de Malthus quando colocamos na equação (I) os limitantes naturais para o crescimento, em geral associados ao próprio crescimento da população (por exemplo, escassez de alimentos ou de espaço). Isto é, denotando por y = y(t) a população em um instante t, o modelo pode ser sintetizado da seguinte maneira
onde b é uma constante positiva e r a taxa de crescimento intrínseco. Esta última equação também é uma EDO e podemos compreendê-la a partir do modelo malthusiano, aqui a taxa de crescimento ideal sofre a interferência dos limites naturais. Isto é, do crescimento ilimitado, r y, subtrai-se um valor que tende a aumentar com o aumento da população, b y2. Em outras palavras, quanto maior a população y, maior será o limite imposto ao crescimento ideal. Resolvendo a última equação obtemos a função que fornece a curva S
 "\mathbf{y = \frac{k}{1+\textit{e}\ ^{a - r\textit{t}}}}\ \ \ \ \ \ \ \ \ \ \ (II)")
onde k é uma constante positiva que representa a capacidade de suporte do meio, r é a taxa intrínseca de crescimento e a é uma constante de ajuste à espécie em questão. Veja no applet abaixo que o gráfico da função definida em (II) é realmente a curva S. Faça um estudo comparativo entre as constantes k, a, r e as fases A, B, C, D, E apresentadas anteriormente no texto "Dinâmica das Populações". Por exemplo, tente observar qual constante altera diretamente a taxa de crescimento, etc. Anote suas conclusões!
Na Figura 2, pode ser observado dois exemplos de crescimento segundo a curva S. Ambos os casos ocorreram em culturas de laboratório.
Figura 2
Para se realizar um estudo mais detalhado de crescimento populacional modelado pela curva S, deveríamos ser capazes de saber quando a ação do meio se sobrepõe ao crescimento e este passa a decair. Ou seja, quando a taxa de crescimento de y com relação ao tempo (ou velocidade de crescimento populacional) que está em ascensão (fase log) começa, sob a ação do meio, a decair. Inciando assim o processo que termina com a estabilização populacional. O ponto da curva onde isto ocorre é chamado de ponto de inflexão, Figura 3. Sabendo que a taxa de crescimento é a derivada, fica fácil encontrar tal ponto. Basta descobrir para qual valor de t a derivada da função logística atinge seu maior valor. Veja no primeiro quadro da Figura 3 a curva de crescimento S com o ponto de inflexão em destaque e ao seu lado, segundo quadro da Figura 3, o gráfico da derivada (taxa ou velocidade de crescimento).
Figura 3
(Adaptação da imagem de Odum e Barret (2007): Fundamentos de Ecologia, página 237.)
Vejamos um exemplo *. Suponhamos que em 1910, na costa do Pacífico dos Estados Unidos, havia uma população aproximada de 1 000 leões marinhos. Após 5 anos observou-se que este número tinha saltado para quase 3 000 animais. O gráfico abaixo nos mostra o crescimento da população de leões marinhos na costa do pacífico dos EUA, a partir de 1910, pelos 30 anos seguintes. Qual é a capacidade de suporte do meio? Clique na caixa "Exibir função" e tente encontrar uma função que se ajuste ao crescimento populacional em questão. Em que momento termina a fase de crescimento acelerado e a taxa de crescimento começa a decair? Qual o ponto de inflexão? Justifique todas as suas respostas!
Crescimento da população de leão marinho na costa do Pacífico dos Estados Unidos
(*) Inspirado no exemplo "Crescimento da população de leão marinho (Costa do Pacífico - USA)".
Comente com o Facebook: